| Fișierul intrare/ieșire | solitar.in, solitar.out | Sursă | ONI 2014 clasa a 8-a |
|---|---|---|---|
| Autor | Rodica Pintea | Adăugată de |
|
| Timp de execuție pe test | 0.1 sec | Limită de memorie | 2048 KB |
| Scorul tău | N/A | Dificultate | N/A |
Vezi soluțiile trimise | Statistici
Solitar (clasa a 8-a)

Se consideră un joc de cărți cu un număr nelimitat de coloane. Inițial, pe prima coloană există, într o ordine oarecare, N cărți cu numere distincte din mulțimea {1,2,…,N}, următoarele coloane fiind vide (fără cărți). Numim secvență de la sfârșitul coloanei ultima sau ultimele două sau ultimele trei etc. cărți din coloană care au scrise pe ele numere consecutive în ordine crescătoare, considerate de jos în sus. De exemplu, în figurile 1 și 2 sunt reprezentate două astfel de coloane cu câte 6 cărți având numere între 1 și 6. În figura 1, secvența de la sfârșitul coloanei este formată doar din cartea 1. În figura 2, secvența de la sfârșitul coloanei este formată din cărțile 3,4 și 5. Se observă că în coloana din figura 1 mai există o secvență formată din cărțile 2, 3 și 4, dar aceasta nu este la sfârșitul coloanei.
Operațiile permise ale jocului sunt:
A. mutarea secvenței de cărți de la sfârșitul unei coloane pe o coloană nouă, dacă acea coloană este vidă (nu conține nicio carte);
B. mutarea secvenței de cărți de la sfârșitul unei coloane la sfârșitul altei coloane cu cărți, doar dacă secvența mutată formează o secvență de numere consecutive cu cele de pe cartea sau cărțile aflate la sfârșitul coloanei respective.
Se dorește ca, printr-un număr minim de operații permise, să se obțină pe una dintre coloane toate numerele de la 1 la N, în ordine crescătoare, considerate de jos în sus.
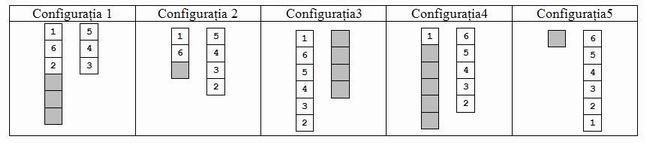
De exemplu, de la configurația inițială din figura 2 se va obține, printr-o operație A, configurația 1 de mai jos. Apoi, printr-o operație B, se obține configurația 2, printr-o nouă operație B se obține configurația 3, apoi se mută secvența 2,3,4,5,6 pe o coloană vidă (operația A), apoi se mută secvența 1 peste secvența 2,3,4,5,6 (operația B) și se obține, pe coloana a doua, configurația finală cerută.
Cerință
Cunoscând valoarea lui N, precum și valorile cărților de pe prima coloană, să se determine numărul minim de operații prin care se poate obține secvența 1, 2, …, N pe una dintre coloane.
Date de intrare
Fișierul solitar.in conține pe prima linie numărul natural N și pe linia următoare N numere naturale distincte din mulțimea {1,2,…,N}, separate prin câte un spațiu, date în ordinea de pe coloană, de sus în jos.
Date de ieșire
Fișierul solitar.out va conține o singură linie pe care va fi scris un număr natural M reprezentând numărul minim de operații prin care se poate obține secvența cerută.
Restricții
- 2≤N≤100000
Exemplu
| solitar.in | solitar.out | Explicație |
|---|---|---|
| 6 1 6 2 5 4 3 |
5 |
Cele 5 mutări sunt descrise în enunțul problemei |
 Poți vedea testele pentru această problemă accesând
Poți vedea testele pentru această problemă accesând
