Fișierul intrare/ieșire	sudoku1.in, sudoku1.out	Sursă	ONI 2013 clasa a 8-a
Autor	Cristina Sichim	Adăugată de	Tudor Coman • tudorcoman
Timp de execuție pe test	0.3 sec	Limită de memorie	40960 KB
Scorul tău	N/A	Dificultate	N/A

Poți vedea testele pentru această problemă accesând atașamentele .

Vezi soluțiile trimise | Statistici

Sudoku1 (clasa a 8-a)

Numim tablou Sudoku o matrice cu n x n elemente ce conține doar cifrele 1, 2 și 3 astfel încât în fiecare pătrat format din 2 × 2 elemente alăturate să existe toate cele 3 cifre și oricare două elemente alăturate pe linie sau pe coloană să fie distincte. Fiecărui tablou Sudoku i se asociază un număr obținut prin scrierea cifrelor în ordine, începând cu prima linie.

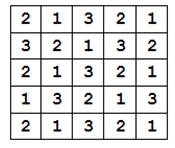
De exemplu, tabloul Sudoku din imaginea alăturată are asociat numărul: 2132132132213211321321321.

Se definește șirul S(n) ca fiind un șir ordonat, format din toate tablourile Sudoku cu n x n elemente, {s₁, s₂, s₃, …}. Pentru orice pereche (s_i, s_j) din S(n) cu i < j, numărul asociat tabloului Sudoku s_i este strict mai mic decât numărul asociat tabloului Sudoku s_j.

Pentru n = 2, șirul S(2) conține, în ordine, tablourile Sudoku:

Cerința

Date fiind două numere naturale n și k să se determine:

• a) numărul tablourilor Sudoku din șirul S(n);
• b) tabloul Sudoku aflat pe poziția k în șirul S(n).

Date de intrare

Fișierul sudoku1.in conține pe prima sa linie două numere naturale n și k separate prin câte un spațiu.

Date de ieșire

Fișierul de ieșire sudoku1.out va conține:

• pe prima linie un număr natural ce reprezintă numărul tablourilor Sudoku din șirul S(n);
• pe următoarele n linii se găsesc câte n cifre, separate prin câte un spațiu, ce reprezintă, în ordine, liniile tabloului Sudoku aflat pe poziția k în șirul S(n).

Restricții

• 2 ≤ n ≤ 32;
• 1 ≤ k < 10¹⁹;
• Pentru rezolvarea corectă a cerinței a) se acordă 20% din punctaj, iar pentru rezolvarea corectă cerinței b) se acordă 80% din punctaj.
• Acordarea punctajului pentru a doua cerință se face numai dacă în fișierul de ieșire există un răspuns pentru prima cerință, indiferent de corectitudinea acestuia.

Exemplu

Explicație

Șirul S(2) conține 12 tablouri Sudoku, pe poziția 6 în șir aflându-se tabloul:
2 1
3 2